对最大后验概率的理解

当一件事情发生时，若某个参数是未知的，我们如何从事件的结果中推测出这个未知的参数呢？
例如，以抛一次硬币为一次实验，重复抛十次，实验结果为：反反反正反反反正反反。
实验结果：X={x1=T，x2=T，……，x10=T}（其中T表示反面朝上，H表示正面朝上）
如何通过实验结果来估计抛一次硬币，正面朝上的概率θ？

极大似然估计法

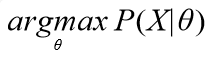
P(X|θ)可看做为一个自变量为θ的函数，求P(X|θ)对于θ的最大值点作为θ的极大似然估计。
因为每次试验都是独立进行的，所以互不相关，概率P(xi|θ)可以直接相乘，等于总概率P(X|θ)。

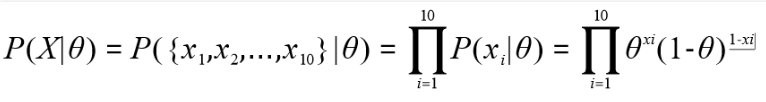)对P(X|θ)取对数使其变为累加

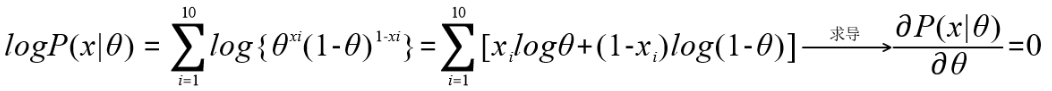通过导函数等于0求出θ=0.2，为θ的极大似然估计值。

最大后验概率

极大似然估计并没有事先考虑θ的分布情况，但根据我们的经验，硬币基本都是均匀的，所以θ取0.5的概率非常大。
这就是θ的先验概率，我们估计θ的值的时候还要把θ的分布考虑进去。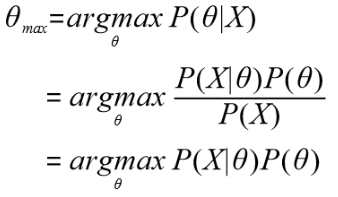

第二个式子是第一个式子用贝叶斯公式展开得到的，P(X)是样本中正面朝上的频率=0.2，是一个定值，与求最大值点的结果无关故舍去。
第三个式子为最终所得式，可以看到最大后验概率只比极大似然估计多乘了一个θ的分布函数。

我们可以把θ的分布看为一个beta分布，则P(θ)可变为: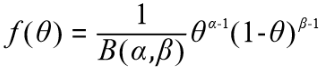

θ是一个连续型随机变量，则P(X|θ)可变为：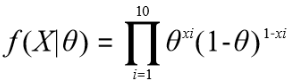

则对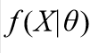

取对数：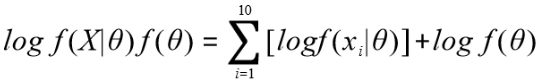

这里可以看出，θ的概率密度函数作为一个附加项也参与了最大值点的求解中，这里和机器学习中的正则化项非常相似。也就是增加了一个约束条件。

两边求偏导，并让其等于0：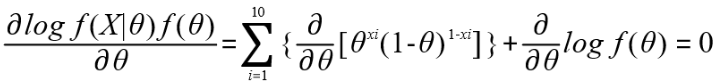

解方程求得 θ 的最大后验概率为：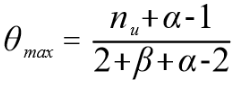

nu为正面朝上次数2。可见最大后验概率中包含了θ密度函数的两个参数，与θ的分布有关。