K-means聚类算法

K-Means

转载

聚类算法有很多种（几十种），K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类。

算法过程

下面，我们描述一下K-means算法的过程，为了尽量不用数学符号，所以描述的不是很严谨，大概就是这个意思，“物以类聚、人以群分”：

1. 首先输入k的值，即我们希望将数据集经过聚类得到k个分组。
2. 从数据集中随机选择k个数据点作为初始大哥（质心，Centroid）
3. 对集合中每一个小弟，计算与每一个大哥的距离（距离的含义后面会讲），离哪个大哥距离近，就跟定哪个大哥。
4. 这时每一个大哥手下都聚集了一票小弟，这时候召开人民代表大会，每一群选出新的大哥（其实是通过算法选出新的质心）。
5. 如果新大哥和老大哥之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止。
6. 如果新大哥和老大哥距离变化很大，需要迭代3~5步骤。

人民代表大会

对于得到的k个分组，计算每个分组内的小弟各元素平均值，作为新大哥。

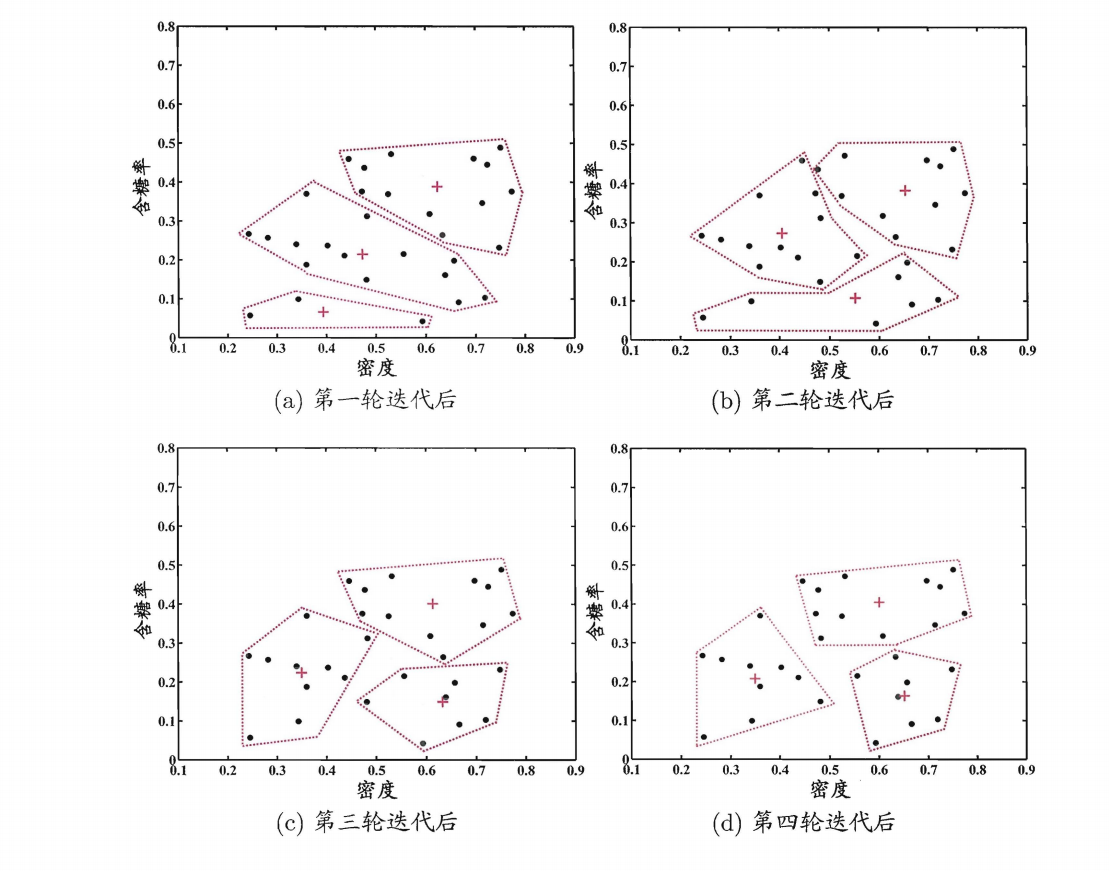
“+”代表每轮的簇平局值，也就是“大哥”。